How Decision Tree Works

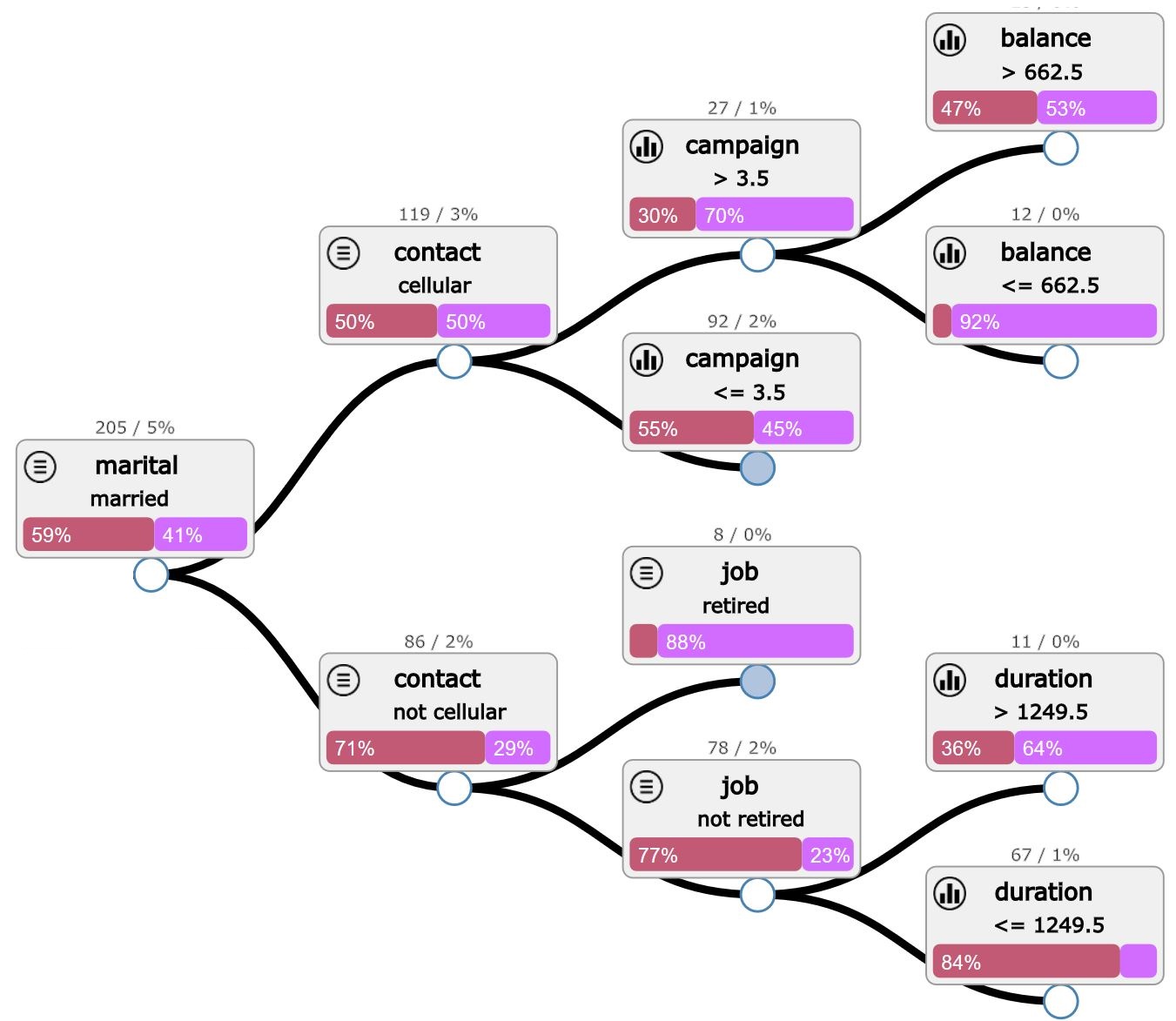
What is a Decision Tree and How Does it Operate?

A decision tree is a graphical representation of possible solutions to a decision based on certain conditions. It is a flowchart-like structure, where each internal node denotes a feature or attribute, each branch represents a decision rule, and each leaf node contains an outcome. The tree is built by recursively splitting the data into subsets based on the most significant attributes until a stopping criterion is reached. This process is often guided by metrics such as entropy and information gain, which help determine the optimal split at each node.

Decision trees are popular in machine learning and data mining due to their simplicity and effectiveness in handling both numerical and categorical data. They can be used for various tasks, including classification, regression, and feature selection. By understanding how decision trees work, one can better appreciate their potential applications and limitations in different contexts.

Key Components of a Decision Tree: Nodes and Edges

A decision tree consists of two primary components: nodes and edges. Nodes represent decisions or questions, while edges represent the possible outcomes or actions. The nodes can be categorized into three types: root, internal, and leaf nodes.

• Root node: This is the initial node in the tree, which represents the entire dataset. It branches out into multiple subsets based on the most significant attribute or feature.
• Internal node: These nodes occur between the root and leaf nodes. They represent the decision-making process based on specific attributes or features. Each internal node has one incoming edge and multiple outgoing edges.
• Leaf node: These nodes occur at the bottom of the tree and represent the final outcomes or decisions. They have no outgoing edges and provide the answer or solution to the decision-making process.

The edges in a decision tree represent the possible outcomes or actions based on the decisions made at each node. They connect the nodes and form the flowchart-like structure of the decision tree. By following the edges from the root node to the leaf nodes, the decision tree guides the user towards a specific outcome or solution.

How Decision Trees Make Decisions: The Role of Entropy and Information Gain

Decision trees use a systematic approach to make decisions based on the concept of entropy and information gain. Entropy is a measure of the impurity or randomness of the data, while information gain quantifies the reduction in entropy after splitting the data based on a specific attribute or feature.

At each internal node, the decision tree aims to find the attribute that maximizes the information gain, thereby minimizing the overall entropy of the system. This process helps ensure that the tree is built in a way that effectively separates the data into homogeneous subsets, leading to accurate predictions and decisions.

For example, consider a dataset with two attributes (A and B) and a target variable (T). The decision tree first calculates the entropy of the target variable (T) for the entire dataset. It then calculates the entropy of T after splitting the data based on attribute A and attribute B. The attribute with the highest information gain (i.e., the largest reduction in entropy) is selected as the splitting attribute for the current node.

By recursively applying this process to each internal node, the decision tree creates a hierarchical structure that guides the user towards a specific outcome or solution based on the optimal sequence of decisions.

Building a Decision Tree: Algorithms and Techniques

Various algorithms and techniques are used for building decision trees, including ID3, C4.5, and CART. Each method has its unique features, advantages, and disadvantages.

ID3 (Iterative Dichotomiser 3)

ID3 is a simple and efficient algorithm that uses a greedy approach to build decision trees based on the concept of information gain. It selects the attribute with the highest information gain as the splitting attribute for each internal node. However, ID3 has some limitations, such as its inability to handle continuous attributes and its susceptibility to overfitting.

C4.5

C4.5 is an extension of ID3 that addresses some of its limitations. It can handle both discrete and continuous attributes by introducing the concept of discretization. C4.5 also uses a more sophisticated method for calculating information gain, which reduces the likelihood of overfitting. However, C4.5 can be computationally expensive and may lead to complex trees with many nodes.

CART (Classification and Regression Trees)

CART is a versatile algorithm that can be used for both classification and regression tasks. It uses a different approach to build decision trees, based on the concept of cost complexity. CART can handle both discrete and continuous attributes and is less prone to overfitting than ID3 and C4.5. However, CART can produce unbalanced trees with many nodes on one side, which may negatively impact its performance.

In summary, decision trees can be built using various algorithms and techniques, each with its strengths and weaknesses. Choosing the right method depends on the specific problem, the nature of the data, and the desired trade-off between accuracy and complexity.

Practical Applications of Decision Trees: From Business to Data Science

Decision trees have a wide range of applications in various fields, including business, finance, healthcare, and data science. Their ability to handle both categorical and numerical data, as well as their interpretability, make them a popular choice for solving complex problems.

Business

In business, decision trees can be used for market segmentation, customer profiling, and sales forecasting. By analyzing customer data, decision trees can help businesses identify different market segments and develop targeted marketing strategies. They can also be used to predict sales trends, helping businesses optimize their inventory and production processes.

Finance

In finance, decision trees can be used for credit scoring, fraud detection, and portfolio optimization. By analyzing financial data, decision trees can help financial institutions assess credit risk, detect potential fraud, and optimize investment portfolios. They can also be used to predict stock prices, helping investors make informed decisions.

Healthcare

In healthcare, decision trees can be used for disease diagnosis, treatment planning, and patient stratification. By analyzing patient data, decision trees can help healthcare providers diagnose diseases, develop personalized treatment plans, and identify high-risk patients. They can also be used to predict patient outcomes, helping healthcare providers optimize their care processes.

Data Science

In data science, decision trees are widely used for classification, regression, and feature selection. They can handle both categorical and numerical data, making them a versatile tool for solving a wide range of data analysis problems. By visualizing the decision-making process, decision trees can also help data scientists gain insights into the underlying patterns and relationships in the data.

In conclusion, decision trees have a wide range of applications in various fields, from business to healthcare and data science. By providing a clear and interpretable representation of the decision-making process, decision trees can help organizations and individuals make informed decisions and solve complex problems.

Advantages and Limitations of Decision Trees: Balancing Pros and Cons

Decision trees are a popular machine learning technique due to their interpretability, scalability, and ability to handle both categorical and numerical data. However, they also have some limitations, such as susceptibility to overfitting and a tendency to become unstable with deep structures.

Advantages

• Interpretability: Decision trees provide a clear and intuitive representation of the decision-making process, making them easy to understand and interpret.
• Scalability: Decision trees can handle large datasets with many features, making them a suitable choice for big data applications.
• Handling mixed data: Decision trees can handle both categorical and numerical data, making them a versatile tool for solving a wide range of data analysis problems.

Limitations

• Overfitting: Decision trees can become overly complex, leading to overfitting and poor generalization performance on new data.
• Instability: Decision trees can be unstable, meaning that small changes in the data can lead to large changes in the tree structure and predictions.
• Bias towards categorical variables: Decision trees can be biased towards categorical variables, leading to poor performance on datasets with mostly numerical features.

To mitigate these limitations, decision trees can be regularized using techniques such as pruning, cross-validation, and ensemble methods. Pruning reduces the complexity of the tree by removing unnecessary nodes, while cross-validation helps prevent overfitting by evaluating the tree on a separate test set. Ensemble methods, such as random forests and gradient boosting, combine multiple decision trees to improve the overall performance and stability of the model.

In conclusion, decision trees have both advantages and limitations. While they are interpretable, scalable, and versatile, they can also be prone to overfitting and instability. By using regularization techniques and ensemble methods, these limitations can be mitigated, leading to more accurate and reliable decision trees.

Decision Trees vs. Other Machine Learning Models: A Comparative Analysis

Decision trees are a popular machine learning technique due to their interpretability, scalability, and ability to handle mixed data. However, they are not the only option available, and it is essential to compare them with other models to determine their unique features and benefits.

Decision Trees vs. Logistic Regression

Logistic regression is a linear model used for classification tasks. It is simple, interpretable, and fast, making it a popular choice for many applications. However, it has some limitations, such as its inability to handle mixed data and its assumption of linearity between the features and the target variable.

Decision trees, on the other hand, can handle mixed data and do not assume linearity. They are also more flexible in terms of the types of relationships they can model, making them a better choice for complex problems. However, they can be more prone to overfitting and may require more computational resources than logistic regression.

Decision Trees vs. Random Forests

Random forests are an ensemble method that combines multiple decision trees to improve the overall performance and stability of the model. They are less prone to overfitting and can handle mixed data, making them a popular choice for many applications.

However, random forests can be more complex and harder to interpret than a single decision tree. They also require more computational resources, making them less suitable for real-time applications. Decision trees, on the other hand, provide a clear and intuitive representation of the decision-making process, making them easier to interpret and understand.

Decision Trees vs. Neural Networks

Neural networks are a powerful machine learning technique that can model complex relationships between the features and the target variable. They are highly flexible and can handle mixed data, making them a popular choice for many applications.

However, neural networks can be more prone to overfitting and may require more computational resources than decision trees. They are also less interpretable, making it harder to understand the decision-making process and identify potential biases or errors.

In conclusion, decision trees have unique features and benefits that make them a valuable tool in the machine learning toolbox. While they may not be the best choice for every problem, they provide a clear and intuitive representation of the decision-making process, making them a popular choice for many applications. By comparing decision trees with other machine learning models, we can better understand their strengths and limitations and make informed decisions about when to use them.

Implementing Decision Trees in Python: A Hands-On Tutorial

Decision trees are a popular machine learning algorithm for classification and regression tasks. They are easy to understand and interpret, making them a great choice for data scientists who want to build transparent models. In this tutorial, we will show you how to build and implement decision trees in Python using popular libraries such as scikit-learn and TensorFlow.

Prerequisites

To follow this tutorial, you should have a basic understanding of Python programming and machine learning concepts. You should also have the following libraries installed:

• NumPy
• Pandas
• Matplotlib
• Scikit-learn
• TensorFlow

Building a Decision Tree with Scikit-Learn

Scikit-learn provides an easy-to-use DecisionTreeClassifier class for building decision trees. Here’s an example of how to use it:

from sklearn.datasets import load_iris from sklearn.tree import DecisionTreeClassifier iris = load_iris()
X = iris.data
y = iris.target
clf = DecisionTreeClassifier()
clf.fit(X, y)

In this example, we loaded the Iris dataset from scikit-learn and split it into features (X) and target (y). We then created a DecisionTreeClassifier object and fit it to the data using the fit() method.

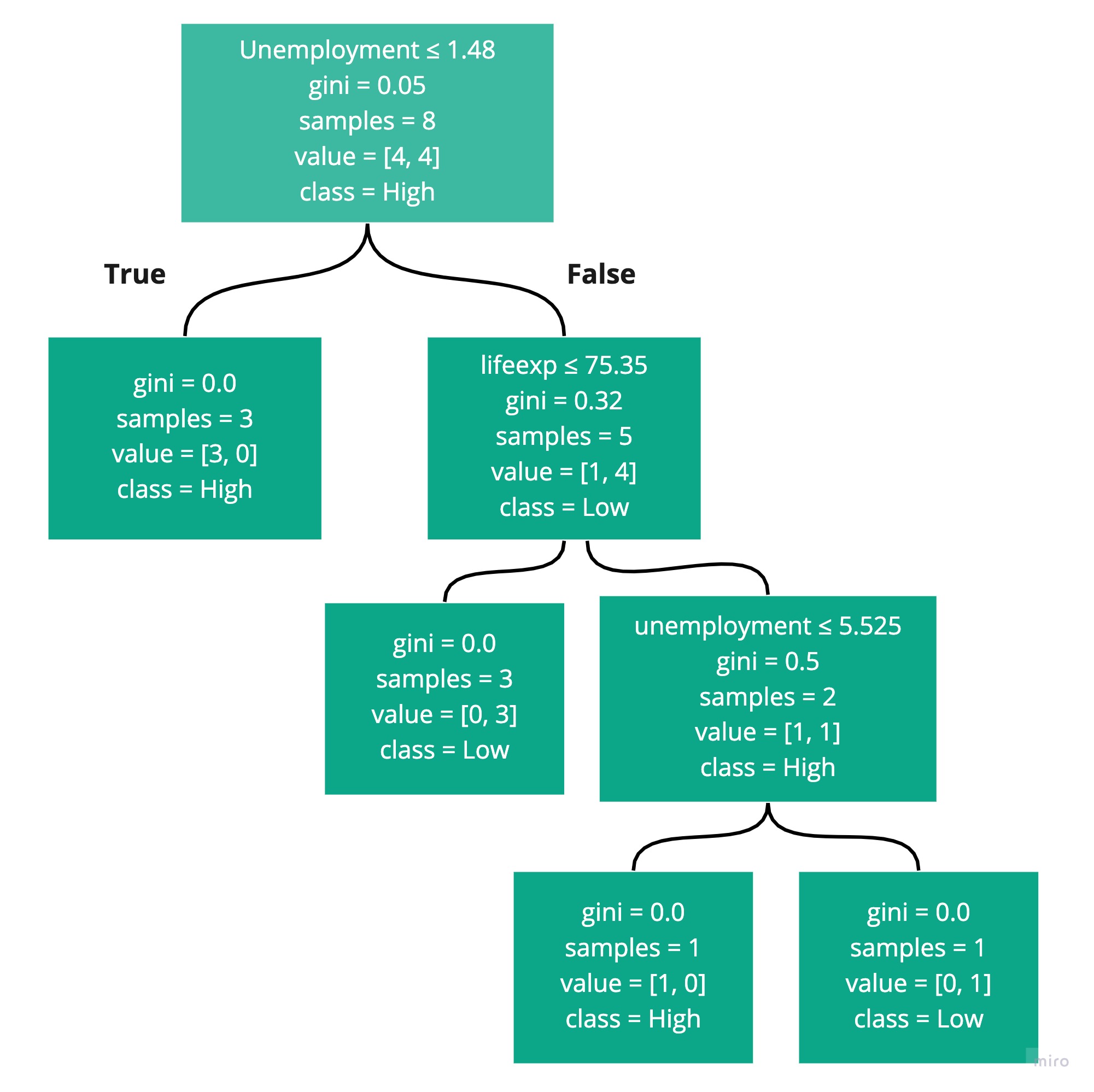
Visualizing a Decision Tree with Scikit-Learn

Scikit-learn also provides a method for visualizing decision trees. Here’s an example:

import matplotlib.pyplot as plt from sklearn.tree import plot_tree fig = plt.figure(figsize=(15,10))
_ = plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()

This will generate a graphical representation of the decision tree, as shown in the following figure.